Adaboost集成学习优化的巷道围岩松动圈预测研究

doi:10.11872/j.issn.1005-2518.2023.03.122

Adaboost集成学习优化的巷道围岩松动圈预测研究

方博扬^,, 赵国彦^,, 马举, 陈立强, 简筝

中南大学资源与安全工程学院，湖南长沙 410083

Prediction Study on Loosening Ring of Surrounding Rock Around Roadways Using the Optimized Ensemble Learning Algorithms Based on Adaboost

FANG Boyang^,, ZHAO Guoyan^,, MA Ju, CHEN Liqiang, JIAN Zheng

School of Resources and Safety Engineering，Central South University，Changsha 410083，Hunan，China

通讯作者: 赵国彦（1963-），男，湖南沅江人，教授，博士生导师，从事采矿、安全与岩石力学研究工作。gy.zhao@263.net

收稿日期: 2022-09-19 修回日期: 2023-03-15

基金资助:

‘十三五’国家重点研发计划课题“深部金属矿绿色开采关键技术研发与示范”. 2018YFC0604606

Received: 2022-09-19 Revised: 2023-03-15

作者简介 About authors

方博扬（1998-），男，湖北孝感人，硕士研究生，从事地压智能监测及灾害控制研究工作591788294@qq.com , E-mail：591788294@qq.com

摘要

为提高巷道围岩松动圈预测准确率，给围岩支护和地压管理提供更科学的指导，提出了一种新的预测方法。采用改进的Adaboost回归算法对3种机器学习算法进行集成优化，即在Adaboost回归算法中寻找误差率阈值的最优值，实现Adaboost全局最优的集成效果。应用网格搜索对BP、SVM和RF的超参数进行优化，建立BP-Adaboost、SVM-Adaboost和RF-Adaboost回归预测模型。结果表明：BP-Adaboost模型的预测性能最好，误差率为7.65%。结合矿山松动圈测试实例进行验证分析，平均相对误差为4.15%。因此，所提出的模型能够为围岩松动圈预测提供参考，可以满足工程应用的需求。

关键词： 围岩松动圈 ; 网格搜索 ; Adaboost算法 ; BP神经网络 ; 支持向量机 ; 随机森林

Abstract

In order to improve the prediction accuracy of loose zone of excavation damaged zone around roadways and provide more scientific guidance for surrounding rock support and ground pressure management，a new prediction method was proposed.The improved Adaboost regression algorithm was used to integrate and optimize three machine learning algorithms，the optimal value of the error rate threshold was found to achieve the global optimal integration of Adaboost.The grid search was used to optimize the hyperparameters of BP，SVM and RF，and the regression prediction models of BP-Adaboost，SVM-Adaboost and RF-Adaboost were established.The results show that the prediction performance of BP-Adaboost is the best，it had the lowest error rate at 7.65 percent.The verification analysis was carried out based on the test example of excavation damaged zone around roadway，the results show that the mean relative error is 4.15%.Therefore，the model proposed in this paper can provide reference for the excavation damaged zone around roadway and meet the needs of engineering applications.

Keywords： loosening ring of surrounding rock ; grid search ; Adaboost algorithm ; Back Propagation Neural Network（BPNN） ; Support Vector Machine（SVM） ; Random Forest（RF）

PDF (2460KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

方博扬, 赵国彦, 马举, 陈立强, 简筝. Adaboost集成学习优化的巷道围岩松动圈预测研究[J]. 黄金科学技术, 2023, 31(3): 497-506 doi:10.11872/j.issn.1005-2518.2023.03.122

FANG Boyang, ZHAO Guoyan, MA Ju, CHEN Liqiang, JIAN Zheng. Prediction Study on Loosening Ring of Surrounding Rock Around Roadways Using the Optimized Ensemble Learning Algorithms Based on Adaboost[J]. Gold Science and Technology, 2023, 31(3): 497-506 doi:10.11872/j.issn.1005-2518.2023.03.122

在浅埋岩体中开挖巷道或隧道卸荷之后，巷道围岩原岩应力的平衡状态受到破坏，其受力状态由三向变成近似两向，致使围岩应力重新分布并产生局部应力集中现象，岩石强度也明显下降，围岩稳定性降低（董方庭，2001；王新丰等，2021）。在深部巷道中，围岩变形量大和岩体承载力低等问题更加普遍，巷道围岩稳定性不仅直接影响正常的施工作业，而且可能会引发冒顶片帮等危险事故（朱川曲，1999）。此外，在巷道的设计与施工中，围岩松动圈是反映围岩应力岩体强度的一个综合性指标，松动圈大小是评价巷道稳定性与支护难易程度的重要因素，而松动圈厚度受诸多因素的影响，如岩石性质和地应力等，因此如何快捷、准确地确定松动圈的大小显得尤为重要。

巷道围岩松动圈厚度研究是一项意义重大的课题，国内外学者已经开展了大量研究工作。在现场实测方面，吴涛等（2015）采用超声波探测技术对围岩松动圈进行测定；伍永平等（2013）和于庆磊等（2021）利用地质雷达技术与相关机理对松动圈厚度进行现场测试。实测法能够直观、相对准确地测量和计算松动圈厚度，但实测费用昂贵，测试条件也复杂多样、难以满足。现阶段测量松动圈厚度较为准确的方法为声波探测法，但由于现实条件和成本的制约，对矿山不同水平上的巷道松动圈厚度进行广泛测量是不现实的。

随着计算机技术和人工智能的发展，越来越多的学者将机器学习和数值分析应用到工程实例中进行理论预测与技术改进。在松动圈理论预测方面，常采用神经网络模型（高玮等，2002；薛新华，2006）、支持向量机模型（Zhou et al.，2011；赵国彦等，2013；朱志洁等，2014）和数值分析方法（陈冲等，2018），取得了较为准确的拟合效果，其中BP神经网络、支持向量机和随机森林模型的应用最为广泛。

集成学习算法Adaboost能够将同一个训练集的不同弱预测器集合成一个强预测器，使弱预测器模型的泛化能力得到改善，鉴于Adaboost优秀的集成能力，有学者采用Adaboost算法预测采空区煤自然发火（赵琳琳等，2018）。

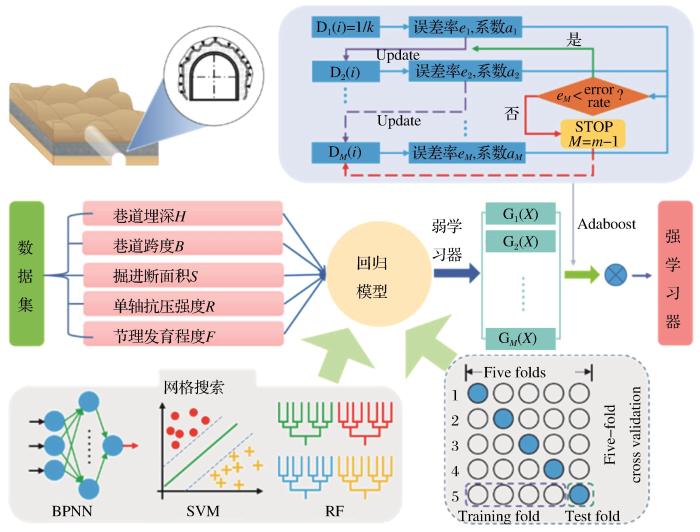
因此，本文将BP神经网络、支持向量机、随机森林模型与Adaboost集成学习相结合，以集成学习模型Adaboost优化以上3种机器学习模型，将弱预测器集合成强预测器，提高预测模型的预测精度和泛化能力。上述模型框架示意图如图1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Adaboost算法优化的3种机器学习方法的围岩松动圈回归预测模型

Fig.1 Regression prediction model of loosening ring of surrounding rock based on three machine learning methods optimized by Adaboost algorithm

1 松动圈厚度预测模型的建立

1.1 松动圈影响因素分析

影响松动圈的因素复杂多样。国内外许多学者对松动圈影响因素进行了探索，结合相关理论分析、相似模拟、现场实测和数值模拟研究（沈金生等，2012；李国盛等，2018），认为围岩松动圈是众多因素综合作用的结果。对于同一矿井的不同位置，由于应力分布不同，其松动圈形状和厚度也不相同。本文结合相关研究对松动圈影响因素进行概括，可以归为2个大类：自然因素和人为因素。自然因素包括围岩强度和围岩压力，围岩强度包括单轴抗压强度（R）、节理裂隙发育程度（F）、地下水和温度等先天自然性质，其中单轴抗压强度（R）是主要影响因素，地下水状态和节理发育程度（F）会对单轴抗压强度（R）有所影响，一定浅埋深范围内温度对围岩的影响较小，可以忽略不计。围岩压力指的是原岩应力场分布的情况，直接影响松动圈的大小。根据岩石弹塑性区理论，不同形状和尺寸的巷道应力场不同，因此围岩压力和巷道形状也有关系，巷道的横截面积和巷道跨度是影响因素之一。围岩应力最直接的体现就是最大主应力及其方向，综合有关工程应用研究的描述，认为巷道的整体应力场状况可由垂直应力和侧应力系数来表述，二者作为松动圈的主要影响因素，可以纳入松动圈量化指标范畴。人为因素则包括掘进方式、支护方式和爆破采动等扰动因素。掘进方式有2种：机械法和钻爆法。机械开挖对松动圈的影响可以忽略不计，相比而言，爆破法对松动圈的影响更大，但相对于松动圈整体厚度来说其扰动范围在浅埋巷道条件下也可以忽略不计。支护方式目前对巷道围岩的作用主要是抵消应力场使围岩应力减小，支护力相对于围岩应力较小，从工程角度来说可以忽略不计。综上各因素分析，从便于定量分析与计算的角度考虑来建立预测模型，确定松动圈厚度的影响因素包括巷道埋深（H）、巷道跨度（B）、掘进断面积（S）、单轴抗压强度（R）和节理发育程度（F）5项指标。理由如下：

（1）巷道埋深（H）。巷道应力场是对围岩松动圈影响最大的因素，而通过力的分解可将应力分布分解为垂直应力和侧向应力。在工程实践中，使用部分仪器测量的应力值实际为二次应力，垂直应力值则更加难以测定且费用昂贵，而H与应力分布具有强相关关系，因此相当一部分松动圈预测模型是用埋深代替应力。在实际工程中，若有测量的垂直应力和侧应力参数时，应当直接使用实际参数，但预估巷道围岩稳定性时，通常没有现场实测应力值，应当优先考虑周边区域的应力估计公式（景锋，2008）。我国大陆地区地应力公式中的最大水平主应力、最小水平主应力和垂直应力均为一次函数的关系，因此使用公式估计的情况下，H能够表示垂直应力和侧应力。

（2）巷道跨度（B）。巷道跨度是指巷道断面跨度，跨度越大，最大垂直应力越大，塑性区面积也越大，巷道围岩破坏程度越大。

（3）掘进断面积（S）。掘进断面积是指巷道的横截面积，断面的形状有矩形、圆形、椭圆形和半圆拱形，其中最常见的是拱形巷道，其面积也容易计算，使用断面积能够统一形状不同的影响，能够作为松动圈定量分析的影响因素之一。

（4）单轴抗压强度（R）。岩石的单轴抗压强度是指岩石破坏的临界压力值，抗压强度越大则岩石受力变形程度越小，松动圈范围越小。

（5）节理发育程度（F）。节理发育程度是对定性指标的量化表示，程度为1表示节理很不发育，2为节理不发育，3为节理一般发育，4为节理较发育，5为节理普遍发育。

1.2 数据集选择与归一化处理

在整合工程实践资料中，收集了66组关于矿区松动圈的基础数据作为样本集，经过查验样本数据均来源于实测数据（表1）。数据的相关系数矩阵如图2所示，其中右上数据表示各指标的皮尔逊相关系数，左下为各影响因素的散点图，从整体数据面分析，H、B、S、R、F这些影响因素是相对独立的，其中H、B、F、L的频率分布近似呈现出正态分布的规律，数据分布范围相对均匀，符合机器学习数据基础，能够避免欠拟合现象。因此，以这5项影响因素作为输入变量进行训练模型。

表1 样本数据

Table 1 Database of samples

样本编号	巷道埋深/m	巷道跨度/m	掘进断面面积/m²	单轴抗压强度/MPa	节理发育程度	厚度/m	样本编号	巷道埋深/m	巷道跨度/m	掘进断面面积/m²	单轴抗压强度/MPa	节理发育程度	厚度/m
1	362	2.6	6.8	62.4	2	0.6	34	689	3.0	7.6	15.1	4	1.8
2	660	4.4	14.6	12.5	5	2.2	35	450	3.0	7.6	11.2	3	1.2
3	384	3.5	11.5	8.5	3	1.2	36	410	3.6	11.7	13.3	4	1.4
4	150	3.6	11.7	14.6	2	0.6	37	348	3.2	9.2	7.5	3	1.2
5	178	2.6	6.4	23.8	3	1.2	38	357	3.2	8.5	10.5	3	1.1
6	510	3.2	7.3	12.6	4	1.6	39	273	2.6	6.6	15.9	2	0.8
7	420	3.6	10.3	14.3	3	1.2	40	280	2.8	7.1	12.7	2	0.8
8	450	3.4	4.8	9.1	5	2.0	41	321	2.6	6.6	15.9	2	0.8
9	236	3.0	7.5	14.3	3	1.2	42	665	4.4	14.6	10.9	4	1.7
10	470	4.0	12.6	10.1	5	2.2	43	350	3.2	8.5	10.5	3	1.2
11	467	3.4	8.2	11.2	3	1.0	44	321	2.6	6.6	9.2	3	1.2
12	490	3.7	8.9	12.5	4	1.8	45	340	3.0	7.6	73.6	2	0.8
13	450	3.6	10.8	13.3	4	1.6	46	470	3.6	11.2	9.1	5	2.1
14	224	3.4	8.2	11.2	3	1.0	47	231	3.0	7.5	18.3	2	0.7
15	460	3.2	9.7	101.6	1	0.4	48	125	3.4	9.8	13.3	3	1.0
16	373	2.5	6.3	14.6	2	0.9	49	296	3.4	7.8	22.4	4	1.4
17	310	2.8	7.1	13.8	3	1.2	50	436	2.8	7.2	15.2	3	1.2
18	125	2.8	7.1	13.3	2	0.7	51	343	3.2	9.6	32.2	2	0.7
19	392	2.8	6.9	14.5	2	0.8	52	525	3.2	7.3	15.8	4	1.6
20	249	3.4	8.2	16.8	3	1.0	53	264	3.2	9.2	11.2	3	1.1
21	140	3.6	10.3	13.4	2	0.5	54	292	3.4	7.8	12.5	4	1.4
22	345	3.0	7.6	65.0	2	0.7	55	362	2.6	6.8	58.0	2	0.8
23	315	2.8	7.1	11.2	3	1.1	56	180	2.8	7.1	110.2	1	0.3
24	550	3.4	9.4	12.5	5	2.1	57	362	2.6	6.8	62.4	2	0.6
25	410	3.2	7.2	13.3	3	1.1	58	340	3.2	9.6	32.2	2	0.7
26	420	3.2	9.2	9.1	4	1.7	59	467	3.4	9.6	10.1	4	1.8
27	340	3.2	9.2	19.8	3	1.3	60	268	3.0	7.5	12.0	3	1.4
28	340	3.2	9.6	32.2	2	0.7	61	236	3.0	7.5	14.3	3	1.2
29	420	3.7	8.9	9.1	4	1.4	62	321	2.6	6.6	13.3	3	1.1
30	370	3.5	8.3	10.5	3	1.0	63	97	3.2	8.8	11.2	4	1.2
31	428	3.6	11.7	16.5	3	1.2	64	322	3.4	7.7	14.3	4	1.5
32	465	4.0	12.6	9.5	4	1.6	65	293	3.5	8.3	11.9	3	1.1
33	403	2.9	7.2	12.6	3	1.3	66	450	3.4	7.8	9.1	5	2.0

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

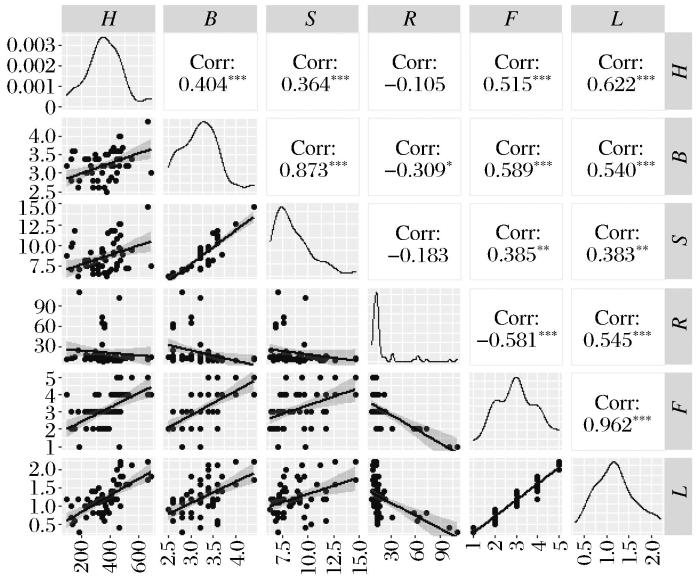
图2 样本散点与相关系数矩阵图

Fig.2 Matrix diagram of sample scatter and correlation coefficient

将数据集的75%作为训练集，25%作为测试集，本文以样本1~50作为训练集，样本51~66作为预测集。即只将前50个样本的数据用于模型的构建，训练时采用五折交叉验证方法避免训练过程的过拟合现象，然后采用后16个样本来验证模型是否准确。将影响松动圈厚度的5项指标作为输入向量 $x_{i} = [x_{i}^{1}, x_{i}^{2}, x_{i}^{3}, x_{i}^{4}, x_{i}^{5}]$ ，以松动圈厚度作为输出向量，建立以BPNN、SVM和RF为基预测器的Adaboost回归预测模型。为了使特征向量具有相同的度量尺度，避免输入向量的量纲和量级不同对预测精度造成影响，使模型输入向量具有更好的映射效果，将全部样本数据输入向量进行归一化处理。

采用以下指标综合评价回归模型的预测能力：

（1）均方误差（MSE）

M S E = \frac{1}{k} \sum_{i = 1}^{k} {(y_{i} - {\overset{⌢}{y}}_{i})}^{2}

（1）

（2）绝对均值误差（MAE）

M A E = \frac{1}{k} \sum_{i = 1}^{k} |y_{i} - {\overset{⌢}{y}}_{i}|

（2）

（3）平均绝对误差百分比（MAPE）

M A P E = \frac{100 %}{k} \sum_{i = 1}^{k} |\frac{y_{i} - {\hat{y}}_{i}}{y_{i}}|

（3）

（4）可解释性方差分数（EVS）

E V S = 1 - \frac{V a r (y_{i} - {\hat{y}}_{i})}{V a r (y_{i})}

（4）

（5）平方相关系数（R²）

R^{2} = 1 - \frac{\sum_{i = 1}^{k} (y_{i} - {\hat{y}}_{i})^{2}}{\sum_{i = 1}^{k} (y_{i} {- \bar{y})}^{2}}

（5）

式中： $\bar{y}$ 为真实值的均值； ${\hat{y}}_{i}$ 为真实值。平方相关系数能反映预测值与实际值的拟合效果， $R^{2}$ 越接近于1代表拟合效果越好。

2 对比模型与参数选择

假设数量为k的样本为 $(x_{1}, y_{1})$ ，…， $(x_{k}, y_{k})$ ，其中 $x_{i} \in R^{N}$ 为N维特征输入向量， $y_{i} \in R$ 为目标输出结果， $i = 1,2, \dots, k$ 。为了考察和验证Adaboost对于该数据集的可行性与准确度，将Adaboost模型分别与BP、SVM、RF回归预测模型结合后的预测结果和指标进行对比，并使用网格搜索对模型参数进行优化。

2.1 BP神经网络

BP神经网络（Back Propagation Neural Network，BPNN）是一种使用误差反向传播算法训练校正连接权的多层前馈神经网络，包含输入层、隐含层和输出层3层结构。该方法采用梯度下降法来计算目标损失函数的最小值，将多维输入特征向量通过网络结构非线性映射出一个（或多个）输出结果并通过迭代逼近期望输出（Zhou et al.，2019）。

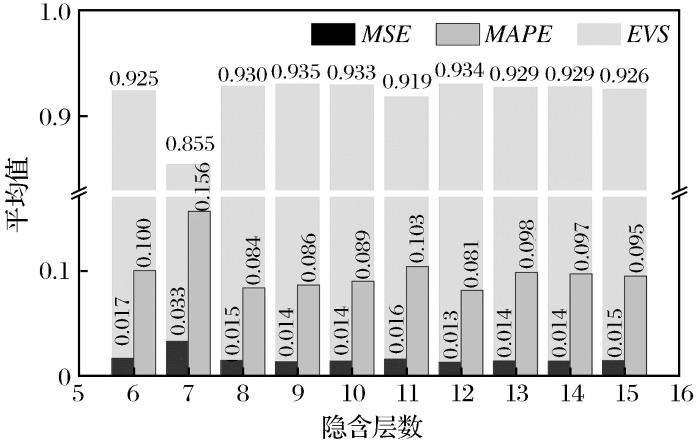
显然，由影响松动圈的5项指标可得神经网络的输入层数目为5，输出层数目为1。通过隐含层数不同的神经网络进行训练，对隐含层数进行网格搜索。使用Python编程分析，设置学习率为0.001，权重与阈值更新的算法选取L-BFGS（Momeni et al.，2020）算法（有限内存拟牛顿算法）加速收敛，设置最大迭代次数为1 000，并对训练集进行五折交叉验证，计算不同隐含层数下5次运算的MSE、MAPE和EVS平均值，结果如图3所示。其中，隐含层数为12时均方误差和平均绝对误差分别为0.013和0.081，此时均方误差最小，预测效果最佳。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 BPNN的网格搜索过程

Fig.3 Grid search process of BPNN

2.2 支持向量机

支持向量机（Support Vector Machine，SVM）同样对解决非线性、小样本、多维数的分类与回归数学问题具有很好的效果，其原理是将空间低维特征向量通过非线性映射至高维特征空间，对转化后的高维空间的特征进行线性分析（朱志洁等，2014）。常使用径向基核（RBF）作为SVM的核函数，影响其性能的参数有惩罚因子C和宽度范围参数γ，现使用网格搜索（Grid Search CV）对参数C和γ进行自动寻优，过程如下：

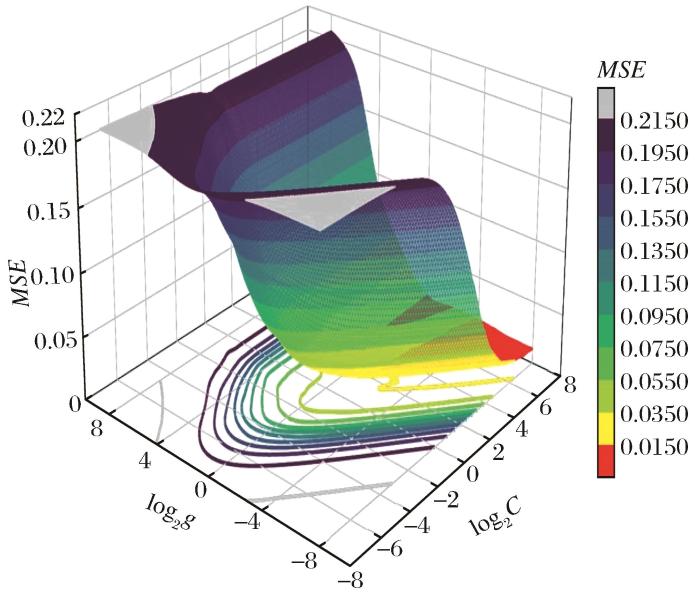
如图4所示利用Python编程对惩罚系数C和宽度参数g进行网格搜索。为了避免结果的偶然性和模型过拟合，采用五折交叉验证方法，计算不同参数下5次运算的MSE平均值。在网格搜索过程中每个网格对应一个搜索结果，通常随着步长的减少将产生更多的网格，同样也会消耗更多的时间，但是搜索范围太小也会陷入局部最小值。通过比较和计算，C和g的搜索范围为（2^-8，2⁸），搜索步长为0.1时，网格搜索的结果更好。通过对log₂C，log₂g的整体观察，C为0.0103、g为64时，误差最小，均方误差MSE达到最小值，此时预测模型的精度最高。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 SVM的网格搜索过程

注：底面曲线图形为曲面等高线投影

Fig.4 Grid search process of SVM

2.3 随机森林

随机森林（Random Forest，RF）是利用决策树构成的一种bagging集成算法，在回归分析中，回归树所集成的森林称为随机森林回归器。其原理与Adaboost相似，利用多个决策树集成一个“森林”式的回归器，再利用Adaboost优化随机森林，将多个“森林”集合成一个大森林。随机森林的主要参数有决策树的数量、深度和特征数量等，本文利用小范围的交叉验证和网格搜索对随机森林的超参数进行自动寻优，最终确定决策树数量为50，深度为5，特征数量为5时，模型的拟合效果最好。

3 改进的Adaboost回归预测算法

Adaboost算法本身是通过改变数据分布来实现的，是一种集成学习模式，提高回归模型预测精度就是根据Adaboost算法原理使用一种或几种回归模型（BPNN、SVM、RF）作为弱预测器（Chao et al.，2020；Xiong et al.，2021）。Adaboost回归算法种类很多，本文采用Adaboost.R2回归算法（景岳等，2021）。该算法根据当前弱预测器训练集的每个样本的权值与预测误差计算其加权误差率来确定下一个弱预测器的样本权值，并依次确定每个弱预测器的权重，最后集合成泛化能力更强的强预测器。Adaboost算法的核心思想是调整错误样本的权重，对弱预测器进行权值寻优并获得最佳的集成效果，其中的回归误差率阈值（3.1节第6步中的误差率）反映了权重调整的程度，不同的回归误差率阈值表示集成的不同程度，合理取值有助于提升模型精度。原Adaboost.R2过程中的回归误差率阈值默认为0.5，本文根据误差率取值对不同模型的集成效果进行研究。均方误差（MSE）是用于回归问题的最常见损失函数，表示预测值和目标值的差值平方和，因此本文以MSE作为集成效果的评判指标，MSE越小，模型的误差越小，集成效果则越好。

3.1 算法实现步骤

第1步：数据归一化得到样本集 $T$ $=$ ｛ $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ ，…， $(x_{k}, y_{k})$ ｝。

x_{i} = \frac{x_{i} - m i n (x_{i})}{m a x (x_{i}) - m i n (x_{i})}

（6）

第2步：通过3.1、3.2、3.3过程的模型与参数选择过程，分别以BPNN、SVM和RF为基学习器得到M个预测器 $G_{1} (x), G_{2} (x), \dots, G_{M} (x)$ 。

第3步：对于 $m = 1,2, \dots, M$ ，使用具有权重D（m）的样本集来计算 $G_{M} (x)$ 的误差率与权重，初始化样本集权重D。

\begin{array}{l} D (1) = (w_{11}, w_{12}, \dots, w_{1 k}); w_{1 i} = \frac{1}{k}; \\ i = 1,2, \dots, k \end{array}

（7）

第4步：计算训练集上的最大误差 $E_{m}$ 。

E_{m} = m a x |y_{i} - G_{m} (x_{i})|, i = 1,2, \dots, k

（8）

第5步：计算每个样本的相对误差 $e_{m i}$ 。

e_{m i} = \frac{|y_{i} - G_{m} (x_{i})|}{E_{m}}

（9）

第6步：计算回归误差率 $e_{m}$ ，弱学习器的系数 $a_{m}$ ，若 $e_{m} \geq$ 误差率，终止训练，令 $M = m - 1$ 。

e_{m} = \sum_{i = 1}^{k} w_{m i} e_{m i}, α_{m} = \frac{e_{m}}{1 - e_{m}}

（10）

第7步：更新样本集的权重分布。

w_{m + 1, i} = \frac{w_{m}}{Z_{m}} {α_{m}}^{1 - e_{m i}}

（11）

式中：规范因子 $Z_{m} = \sum_{i = 1}^{k} w_{m i} a_{m}^{1 - e_{m i}}$ 。

第8步：输出强预测器 $H (x)$ 。

H (x) = \underset{1 \leq m \leq M}{\underset{︸}{m e d i a n}} [l n \frac{1}{α_{m}} G_{m} (x)]

（12）

式中： $m e d i a n$ 表示中位数； $H (x)$ 是以 $l n \frac{1}{a_{m}}$ 为权重的所有弱学习器的加权中位数。

3.2 预测结果分析

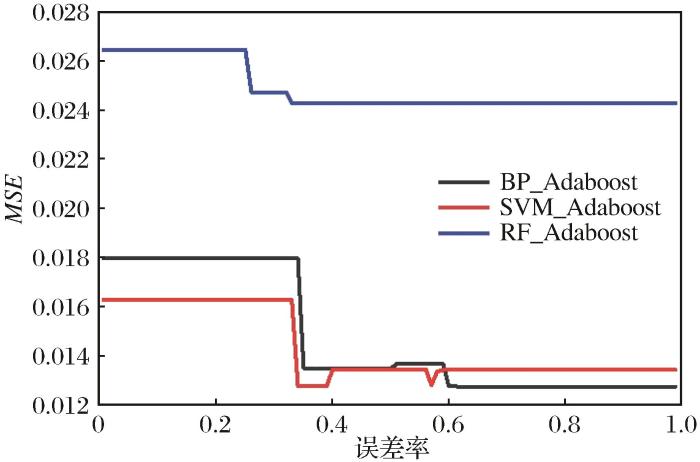
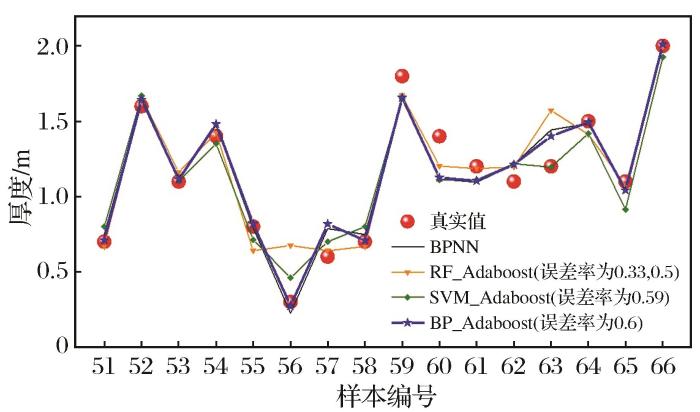
为了探究误差率阈值对不同模型性能的影响，分别将BP、SVM和RF模型作为基学习器代入Adaboost模型中运算，为保证基学习器数量充足，取基学习器的数量为100，然后计算不同回归误差率阈值下模型均方误差MSE的大小，得到图5所示的回归误差率阈值的参数寻优过程。图5表明了各模型预测性能随误差率变化的情况，随着误差率的增加，Adaboost模型具有误差更小的趋势且最终达到收敛效果。图5表示BPNN、SVM和RF模型分别在误差率为0.60、0.59和0.33时达到的最佳效果。然后将得到的最优参数代入模型进行预测，最终得到不同误差率参数下BPNN、SVM和RF模型的预测值，各模型的评价指标如表2所示。由表2可知，当误差率阈值为0.60时，BP_Adaboost模型的MSE最小，为0.127，集成学习优化效果最好的模型为BP_Adaboost。各模型的预测值与厚度的实际值大小如图6所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 误差率参数寻优过程

Fig.5 Parameter optimization process of error rate

表2 不同预测模型评价指标对比（测试集）

Table 2 Comparison of evaluation indexes for different prediciton models（testing set）

模型	误差	MSE	R²	MAE/%
BPNN	-	0.01527	0.923	9.83
BP_Ada	0.50	0. 01376	0.931	8.05
BP_Ada	0.60	0.01273	0.936	7.65
SVM	-	0.01412	0.928	10.81
SVM_Ada	0.50	0.01344	0.932	10.29
SVM_Ada	0.59	0.01318	0.933	9.58
RF	-	0.02325	0.882	15.36
RF_Ada	0.33	0.02473	0.877	15.13
RF_Ada	0.50	0.02473	0.877	15.13

新窗口打开| 下载CSV

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 真实值与不同模型的预测值（测试集）

Fig.6 Aactual values and predicted values of different models（testing set）

3.3 工程实例

为了验证本文模型的有效性，选取2个矿山3个巷道的实测数据（经查验所选数据与训练集未重合），使用误差率阈值为0.60的BP_Adaboost模型进行验证分析，相关物理量见表3。

表3 松动圈厚度实测值与计算值的对比

Table 3 Comparison between calculated values and measured values of thickness of loosening ring

序号

矿山名称

H/m

B/m

S/m²

R/MPa

实际值/m

预测值/m

相对误差/%

实例一

三山岛金矿

600

3.8

14.2

71.26

1.10

1.16

5.45

实例二

大顶山矿区

420

3.6

7.8

14.30

1.10

1.12

1.82

实例三

141

3.2

7.8

37.90

1.35

1.42

5.18

新窗口打开| 下载CSV

实例一是位于山东省莱州市的三山岛金矿。钱振宇等（2013）使用声波检测仪对三山岛金矿-600 m采场巷道北巷子进行测量，该拱形巷道宽度为3.8 m，高度为4 m，面积估算为14.2 m²，实测松动圈厚度平均值为1.1 m。

实例二和实例三是位于四川省凉山州西昌市的大顶山矿区。大顶山矿区山峰顶海拔为3 280 m，巷道平均埋深为755 m，垂直地应力约为20 MPa。王伟（2014）使用一发双收声波仪对大顶山2 510分层的14#进路的巷道断面进行测量，巷道断面为2.8 m×2.8 m，测得断面1顶板孔松动圈厚度为1.1 m，断面2顶板孔松动圈厚度为1.35 m。

利用调好参数和训练好的BP_Adaboost模型对以上工程实例进行再验证，松动圈厚度值的计算结果见表3。由表3可知，三山岛金矿松动圈厚度的预测值与现场实测值的相对误差为5.45%；大顶山矿区2个巷道的预测值与实际值的相对误差分别为1.82%和5.18%。实例一和实例三的误差率和预测集平均误差率相当，而实例二的预测误差相比其他2个工程实例较小。分析其原因，H集中分布在400 m范围内（图2），当预测数据处于训练集分布频率较高范围时，机器学习模型的预测性能就越好，因此本模型对于埋深400 m左右的实例预测精度更高。在巷道某一区段的松动圈厚度会在一定范围内波动，破裂范围具有一定的模糊性，实际试验测得的松动圈厚度为范围内平均值，具有最高的可信度。本文提出的模型在上述工程实例预测中的误差较小，能够满足工程要求，故上述模型可用于巷道松动圈的预测。

4 结论

（1）采用Adaboost算法分别对BP神经网络、支持向量机和随机森林模型进行了集成优化，提高了各模型的预测精度，并将各模型进行对比分析，发现BP_Adaboost模型在误差率阈值为0.6时精度最高，误差最小，绝对均值误差为7.65%。结合2个矿山现场的实测数据，对BP_Adaboost模型进行验证，得到3个验证实例的误差分别为5.45%、1.82%和5.18%，平均误差达到4.15%，预测结果与实测结果之间的误差偏小，说明该模型能够对松动圈的厚度进行预测并满足工程需求，为评价巷道围岩稳定性和支护难易程度提供指导。

（2）改进了Adaboost算法，引入Adaboost回归算法中对回归误差率阈值error rate的网格搜索，探究了Adaboost中误差率阈值对集成效果的影响，提高了Adaboost.R2的回归集成效果，提高了模型预测精度。

（3）数学模型法受制于影响因素考虑不足及现有数据库噪声等条件而难以提高预测精度。本文仅综合考虑了5项指标，旨在从算法与计算的角度提高模型的预测精度，然而松动圈的厚度受到多种因素的共同影响，后续可考虑引入更多的影响因素，引入修正系数或进一步考虑时间效应等方法提高该预测方法的准确度与普适性。

http://www.goldsci.ac.cn/article/2023/1005-2518/1005-2518-2023-31-3-497.shtml

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[]

Chao

， Kim

，2020.

Brain image segmentation based on the hybrid of back propagation neural network and Adaboost system

［J］.Journal of Signal Processing Systems for Signal Image and Video Technology，92（3）：289-298.