库水位骤降耦合不同类型降雨泥岩边坡渗透稳定性数值模拟研究

doi:10.11872/j.issn.1005-2518.2018.05.647

库水位骤降耦合不同类型降雨泥岩边坡渗透稳定性数值模拟研究

彭博^,

1 西南交通大学土木工程学院，四川成都 610000

Numerical Simulation Study of Seepage Stability of Mudstone Slope with Dif-ferent Rainfall Types Coupled with Sudden Drop of Reservoir Water Level

PENG Bo^,

1 College of Civil Engineering，Southwest Jiaotong University，Chengdu 610000，Sichuan， China

收稿日期: 2018-08-02 修回日期: 2018-09-21

基金资助:

国家自然科学基金项目“深部工程高应力型软岩流变扰动的分数阶导数建模”. 61503201

Received: 2018-08-02 Revised: 2018-09-21

作者简介 About authors

彭博（1989-），男，四川成都人，工程师，从事建筑设计及其理论研究工作 , E-mail：2373252023@qq.com

摘要

为研究泥岩边坡在库水位骤降与不同降雨类型耦合情况下的渗流特性和稳定性规律，基于岩体非饱和理论和Hoek-Brown准则，利用极限平衡理论推导出库水位与降雨耦合情况下的边坡稳定系数表达式，并利用Geo-slope软件对泥岩边坡进行数值模拟。结果表明：（1）库水位骤降情况下，孔压先减小后保持不变，监测点距库岸越远，孔压的变化幅度越小，边坡稳定系数随时间变化呈现先减小后增大，之后保持不变的规律，库水位下降速率越大，最小稳定系数越小，且其出现的时间越早；（2）不同静库水位耦合不同类型降雨情况下，孔压先增大后减小，静库水位越高，整体孔压越大；（3）库水位骤降偶遇降雨边坡内部的孔压逐渐减小，在降雨过程中陡然上升，当平均型降雨发生在库水位骤降第24~26 d时，最小稳定系数达到最小。该研究成果为正确认识降雨耦合库水位骤降情况下的岩质边坡稳定性规律提供了参考。

关键词： 库水位骤降 ; 不同类型降雨 ; 泥岩质边坡 ; 渗透稳定 ; Geo-slope软件 ; 数值模拟

Abstract

In order to study the seepage characteristics and stability law of mudstone slope under the coupling of sudden drop of reservoir water level and different rainfall types，based on the unsaturated rock mass theory and Hoek-Brown criterion，the expression of slope stability coefficient under the coupling of reservoir water level and rainfall was derived by using limit equilibrium theory，and numerical simulation of mudstone slope was carried out by using Geo-slope software.The results show that the pore pressure decreases first and then remains unchanged when the reservoir water level drops suddenly.The farther the monitoring point is from the reservoir bank，the smaller the variation amplitude of pore pressure is.The slope stability coefficient decreases first and then increases with time，and then remains unchanged.The larger the reservoir water level dropping rate is，the smaller the minimum stability coefficient is and the earlier it occurs.The pore pressure increases first and then decreases under the condition of different static reservoir water level coupling different types of rainfall.The higher the static reservoir water level is，the larger the overall pore pressure is.When the reservoir water level drops suddenly and encounters occasional rainfall，the overall trend of pore pressure in slope decreases gradually and rises abruptly in the process of rainfall.The minimum stability coefficient is the smallest when the mean rainfall occurs at the 24~26 d of the sudden drop of the reservoir water level.The research results provide a reference for correctly understanding stability law of rock slope under the condition of sudden drop of reservoir water level coupled with rainfall.

Keywords： sudden drop of reservoir water level ; different types of rainfall ; mudstone slope ; seepage stability ; Geo-slope software ; numerical simulation

PDF (2872KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

彭博. 库水位骤降耦合不同类型降雨泥岩边坡渗透稳定性数值模拟研究[J]. 黄金科学技术, 2018, 26(5): 647-655 doi:10.11872/j.issn.1005-2518.2018.05.647

PENG Bo. Numerical Simulation Study of Seepage Stability of Mudstone Slope with Dif-ferent Rainfall Types Coupled with Sudden Drop of Reservoir Water Level[J]. Gold Science and Technology, 2018, 26(5): 647-655 doi:10.11872/j.issn.1005-2518.2018.05.647

库水位骤降和降雨是影响边坡稳定的2个重要因素^[1,2,3,4,5]，其对边坡的影响主要体现在2个方面：一是库水位骤降会导致距离库岸较远处浸润线下降，出现“滞后”现象^[6,7,8]，从而加剧下滑力；二是降雨导致土体内部的孔隙水压力升高，土体有效应力减小，强度参数降低^[9,10,11]。降雨和库水位骤降导致边坡失稳的危害有：第一，对库区周围的水工建筑物造成永久性破坏；第二，对库区周边居民的生命财产安全造成威胁；第三，对库区的有效库容造成影响，因此对库水位和降雨联合情况下的边坡渗透稳定性开展研究具有重要意义。

国内学者对库水位和降雨联合情况下的边坡渗透稳定性开展了若干研究，例如：郭子正等^[12]利用灰色模型对三峡库区某堆积滑坡体进行了库水位和降雨联合作用下的安全性评价；方景成等^[13]针对库水位骤降速率和降雨强度2个因素，对边坡稳定性进行了单因素敏感性分析；唐扬等^[14]利用HYDRUS-1D软件对三舟溪边坡降雨和库水位变动进行了模拟；王一兆等^[15]对降雨入渗条件下边坡深层与浅层的渗流特性及稳定性进行了探讨。然而，上述研究主要针对土质边坡，对于岩质边坡在库水位和降雨耦合情况下的边坡渗透稳定性研究鲜有报道。

1980年，Hoek等^[16,17]结合岩石性状方面的理论研究和实践经验，基于Griffith脆性断裂理论，创造性地提出了迄今为止应用极为广泛的岩石强度准则——Hoek-Brown强度准则，可综合考虑岩体各方面的特性。本文在曾铃等^[18]开展的泥岩边坡稳定性研究基础上，进一步基于极限平衡理论，推导了考虑岩体边坡非饱和特性和损伤特性情况下的泥岩边坡稳定系数公式，以三峡库区某泥岩质边坡体模型为例，对库水位和不同类型降雨耦合情况下的边坡渗透稳定性进行了研究，以期为相应工况下的边坡渗透稳定性认识提供参考。

1 考虑非饱和及损伤的边坡渗透稳定性理论

1.1 非饱和渗流理论

以压力水头表示的饱和—非饱和微分方程可表示为：

\frac{\partial}{\partial x_{i}} [{k_{i j}}^{s} k_{r} (h_{c}) \frac{\partial h_{c}}{\partial x_{j}} + k_{i 3} k_{r} (h_{c})] + Q = [C (h_{c}) + \frac{θ}{n} S_{s}] \frac{\partial h_{c}}{\partial t}

（1）

式中：k_ij为饱和渗透张量；k_r为相对透水率；h_c为压力水头；Q为源汇项；C（h_c）为容水度；θ为与压力水头相关的函数；n为土体内部的孔隙率；S_s为单位贮水量。

1.2 基于Hoek-Brown准则的强度参数推导

2002年，Hoek等^[16]提出了最新的Hoek-Brown准则，表达式为

σ_{1} = σ_{3} + σ_{c} (m_{b} {\frac{σ_{3}}{σ_{c}} + s)}^{a}

（2）

式中：σ₁、σ₃分别为岩体破坏时的最大和最小有效主应力（kPa）；σ_c为岩体单轴抗压强度（kPa）；m_b、s为与岩体特性有关的参数；a为曲线参数。其中，m_b可表示为

m_{b} = m_{i} e x p \frac{(G S I - 100)}{(28 - 14 D)}

（3）

式中：m_i为岩体性状；GSI为地质强度指标，范围为0~100；D为岩体损伤因子，范围为0~1。

s可表示为

s = e x p (\frac{G S I - 100}{9 - 3 D})

（4）

a可表示为

a = 0.5 + (e^{- G S I / 15} - e^{- 20 / 3})

（5）

为便于参数转换，将Hoek-Brown准则的包络线绘制于主应力坐标内，不同应力水平下的包络线切线方程等价于相同应力下的Mohr-Coulomb准则^[19]，如图1所示。Mohr-Coulomb准则可表示为

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Hoek-Brown准则包络线及Mohr-Coulomb切线

Fig.1 Hoek-Brown criterion envelope and Mohr-

Coulomb tangent

σ_{1} = \frac{1 + s i n ϕ}{1 - s i n ϕ} \cdot σ_{3} + \frac{2 c \cdot c o s ϕ}{1 - s i n ϕ}

（6）

式中： $ϕ$ 为内摩擦角，在应力水平为σ_a处的切线方程为

σ_{1} = k σ_{3} + b

（7）

式中：k为Mohr-Coulomb切线的斜率（图1），b为Mohr-Coulomb切线与σ₁主应力轴的交点纵坐标值，本文中GSI≥45，为方便推导，可将式（5）中a值近似为0.5，得到Mohr-Coulomb切线的k值与b值：

k = 1 + \frac{m_{b} σ_{c}}{2 (σ_{b} - σ_{a})}

（8）

b = \frac{2 c \cdot c o s ϕ}{1 - s i n ϕ}

（9）

对照式（6），根据式（8）、（9）可得对应于Mohr-Coulomb准则下的 $ϕ$ 值和c值：

ϕ = 2 t a n^{- 1} \sqrt[]{1 + \frac{m_{b} σ_{c}}{2 \cdot (σ_{b} - σ_{a})}} - 90^{°}

（10）

c = b \cdot \frac{1 - s i n ϕ}{2 c o s ϕ}

（11）

式（10）、（11）即为基于Hoek-Brown准则下的等效黏聚力与内摩擦角表达式。

1.3 考虑非饱和效应的Hoek-Brown抗剪强度推导

对于考虑非饱和效应的抗剪强度计算，多采用Drnevich等^[20]提出的非饱和抗剪强度理论，表达式为

τ_{f} = c + (σ - u_{a}) t a n φ + (u_{a} - u_{w}) t a n φ_{b}

（12）

式中：τ_f为土体实时抗剪强度，c、φ为有效强度参数；σ为法向总应力与孔隙气压力的差值；u_a为孔隙空气压力，本文中u_a=0；u_w为孔隙水压力；φ^b表征由负孔隙水压力而提高的强度。

将式（10）、（11）代入（12），得到基于Hoek-Brown准则下的非饱和抗剪强度计算公式：

τ_{总} = b \cdot \frac{1 - s i n (2 t a n^{- 1} \sqrt[]{1 + \frac{m_{b} σ_{c}}{2 \cdot (σ_{b} - σ_{a})}} - 90^{\circ})}{2 c o s (2 t a n^{- 1} \sqrt[]{1 + \frac{m_{b} σ_{c}}{2 \cdot (σ_{b} - σ_{a})}} - 90^{\circ})} - u_{w} t a n φ_{b} + σ t a n ϕ = c_{总} + σ t a n ϕ

（13）

式中：c_总为基于Hoek-Brown准则下的非饱和黏聚力，可表示为

c_{总} = b \cdot \frac{1 - s i n (2 t a n^{- 1} \sqrt[]{1 + \frac{m_{b} σ_{c}}{2 \cdot (σ_{b} - σ_{a})}} - 90^{°})}{2 c o s (2 t a n^{- 1} \sqrt[]{1 + \frac{m_{b} σ_{c}}{2 \cdot (σ_{b} - σ_{a})}} - 90^{°})} - u_{w} t a n φ_{b}

（14）

1.4 基于Hoek-Brown准则非饱和稳定系数公式

边坡稳定性理论采用Biship公式，结合式（13），得到基于Hoek-Brown准则下考虑非饱和效应的极限平衡稳定系数公式：

F S = \frac{1}{\sum W s i n α} \sum [\frac{c_{总} β + W t a n ϕ - \frac{c_{总} β}{F S} s i n α \cdot t a n ϕ}{m_{α}}]

（15）

式中： $F S$ 为稳定系数；c_总为基于Hoek-Brown准则下的非饱和黏聚力；β为滑块的底边长度；W为土条的重量；α为土条底面的倾斜角；φ为土体的内摩擦角。m_α可表示为

m_{α} = c o s α + \frac{s i n α \cdot t a n α}{F S}

（16）

2 计算模型及计算参数

2.1 计算模型及边界条件

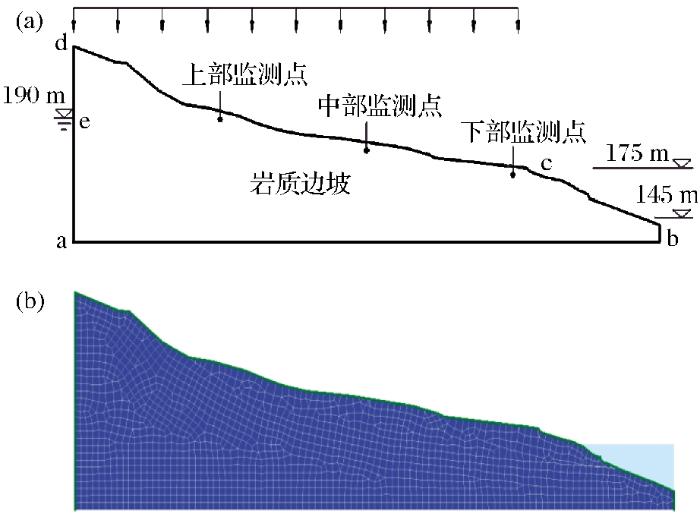
计算模型采用三峡库区某泥岩质边坡体模型，正常蓄水位为175 m，死水位为145 m，平均坡度约为13°，边坡典型剖面图如图2（a）所示。网格剖分为四面体单元和三角形单元，全局共剖分为865个节点，897个单元，模型网格剖分图如图2（b）所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 计算模型及网格划分

Fig.2 Computational model and mesh generation

计算边界条件设置如下：ae为零流量边界；de、ab为不透水边界；bc为库水位变动边界，变化范围为145~175 m，库水位根据三峡地区长期运行经验，分别取0.5，1.0，1.5 m/d进行计算分析；dc为降雨流量边界。

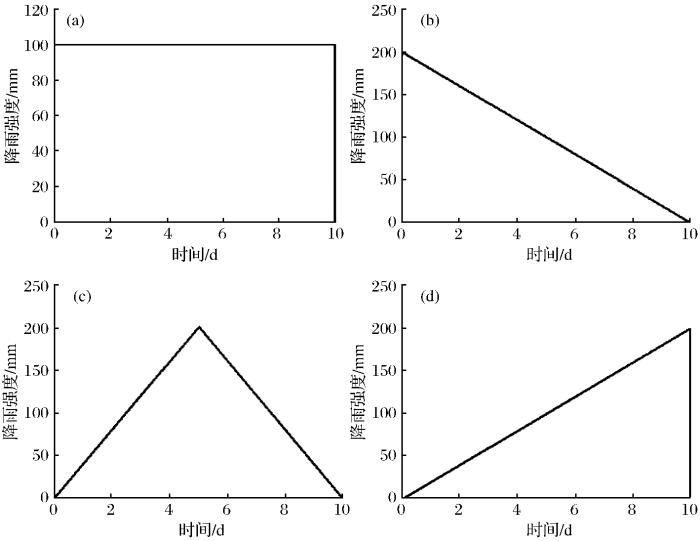
为突出不同类型降雨联合库水位变动情况下的泥岩岩质边坡的渗透稳定性变化规律，选取典型的峰值降雨（即平均型降雨、前锋型降雨、中锋型降雨和后锋型降雨），不同类型降雨时程曲线见图3。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同类型降雨时程曲线

（a）平均型降雨；（b）前峰型降雨；（c）中峰型降雨；（d）后峰型降雨

Fig.3 Time history curves of different type rainfall

2.2 计算工况

计算工况选取：工况1，无降雨条件下的库水位不同骤降速率；工况2，不同静库水位水平下的耦合不同类型降雨；工况3，平均型降雨发生在库水位骤降的不同时刻。具体计算工况见表1。

表1 计算工况

Table 1 Calculation conditions

编号	计算工况	库水位		降雨
编号	计算工况	库水位/m	下降速度/（m·d^-1）	降雨类型	发生时刻/d
工况3	平均型降雨发生在库水位骤降的不同时刻	175→145	0.5	a	0～2 12～14 24～26 36～38 48～50
工况1	无降雨条件下的库水位不同骤降速率	175→145	0.5
			1.0
			1.5
工况2	不同静库水位水平下的耦合不同类型降雨	155	0	a，b，c，d	0～10
		165	0	a，b，c，d	0～10
		175	0	a，b，c，d	0～10

a，b，c，d分别代表平均型、前峰型、中峰型和后峰型降雨

新窗口打开| 下载CSV

2.3 计算参数

结合地质勘探资料和室内试验结果，得到岩体的物理力学性能指标如下：岩体的饱和渗透系数k_sat=8.84×10⁻⁷m/s，饱和重度γ_sat=26.5 kN/m^-3，有效黏聚力c $'$ =10.5 kPa，有效内摩擦角 $ϕ$ '=15.6°， $ϕ$ ^b=12°，饱和体积含水率θ_s=0.1 m³/m³，非饱和Fredlund&Xing参数a=12 kPa，m=1.5，n=1。

3 计算结果分析

3.1 工况1渗透稳定性分析

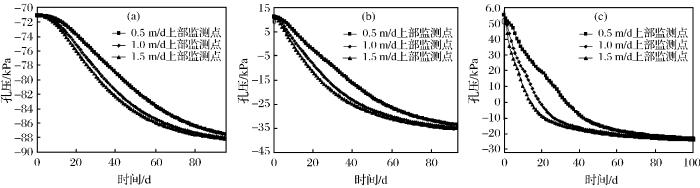
在无降雨的库水位不同骤降速率（0.5，1.0，1.5 m/d）情况下，不同监测点的孔压变化规律如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同库水位骤降速率下不同监测点的孔压变化

（a）上部监测点；（b）中部监测点；（c）下部监测点

Fig.4 Pore pressure variation of different monitoring points under different water level sudden drop rates

总体上，孔压随库水位下降呈现先减小后保持不变的趋势。上部监测点孔压呈现先保持不变后加速减小，之后再保持不变的趋势；中部监测点孔压与上部监测点变化规律相似，但是在前期孔压下降的时间较提前；下部监测点孔压呈现前期迅速减小，在库水位下降结束后几乎保持不变的规律。随着边坡体内的监测点距库岸越远，孔压的变化幅度越小。

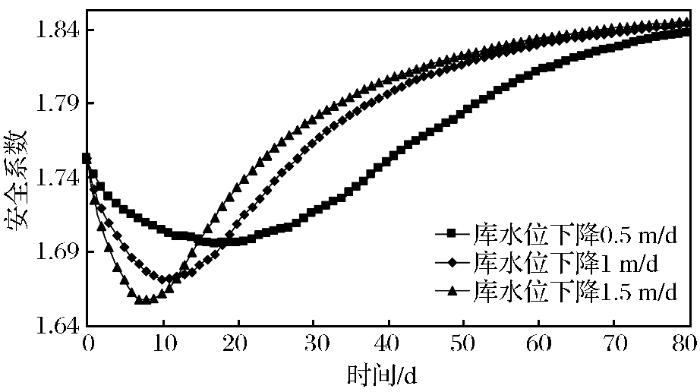
不同库水位下降速率情况下的稳定系数变化规律如图5所示。由图可知，在不同库水位骤降速率下，边坡稳定系数总体上随时间呈现先减小后增大，最后保持不变的规律，库水位下降速率越大，最小稳定系数越小且最小稳定系数出现的时间越早。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同库水位下降速率下稳定系数变化

Fig.5 Variation of safety factor under different water level drop rates

3.2 工况2渗透稳定性分析

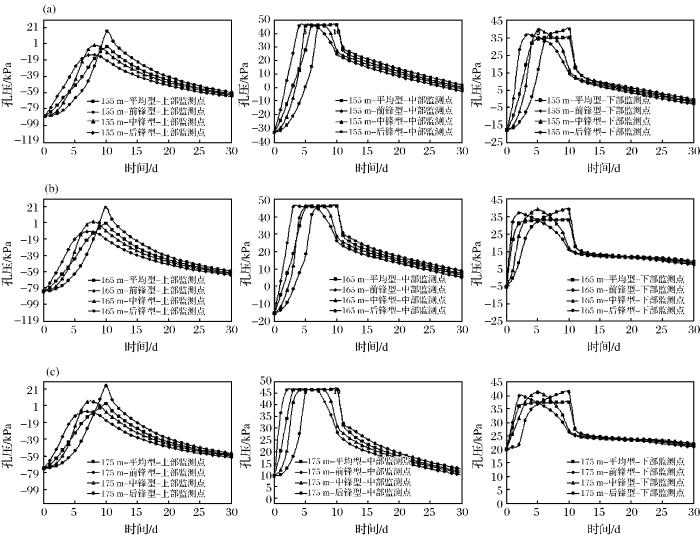
不同静库水位水平（库水位为155，165，175 m）下耦合不同类型降雨情况下的不同监测点孔压变化规律如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同静库水位水平下耦合不同类型降雨情况下的不同监测点孔压变化规律

（a）库水位为155 m；（b）库水位为165 m；（c）库水位为175 m

Fig.6 Variation of pore pressure at different water levels of different static reservoirs coupled with different types of rainfall and different monitoring points

不同监测点在不同降雨类型条件下，孔压呈现先增大后减小的规律，与工况1相比，在降雨时刻的孔压有个突然上升的趋势。对于不同监测点来说，孔压达到最大的时刻略有差异，以静库水位为165 m为例，对于上部监测点，最大孔压达到最大的时间先后顺序分别是前锋型、中锋型、后峰型和平均型，其中平均型达到的最大孔压最大，其次为中锋型与后峰型，前锋型最小；对于中部监测点，最大孔压达到最大的时间先后顺序分别为前锋型、中锋型、后峰型和平均型，4种降雨类型所达到的最大孔压并无差异；对于下部监测点，最大孔压达到最大的时间先后顺序分别为前锋型、中锋型、后峰型和平均型，前锋型、中锋型和后峰型降雨最大孔压较一致，而平均型降雨最大孔压较小。对于不同静库水位（155，165，175 m）来说，静库水位越高，整体孔压越大。

3.3 工况3渗透稳定性分析

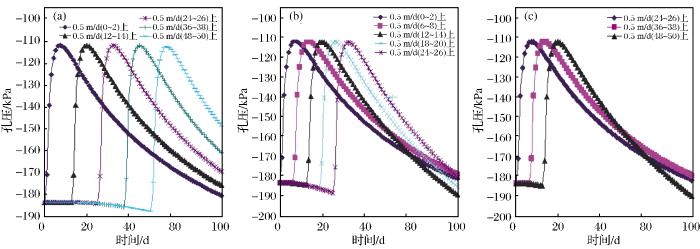
平均型降雨发生在库水位骤降的不同时刻（0~2，12~14，24~26，36~38，48~50 d）时不同监测点的孔压变化规律如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同监测点的孔压变化

（a）上部监测点；（b）中部监测点；（c）下部监测点

Fig.7 Pore pressure variation at different monitoring points

由图7可知，库水位骤降情况下，边坡内部的孔压总体上逐渐减小，与工况1和工况2相比，降雨发生在不同时刻均会导致该时刻的孔压有突然上升的趋势，但是在边坡内部不同监测点上升幅度差异较大。上部监测点平均上升幅度为76 kPa，中部监测点平均上升幅度为17 kPa，而下部监测点平均上升幅度为4.3 kPa。因此，孔压上升幅度大小排序为上部监测点≥中部监测点≥下部监测点。

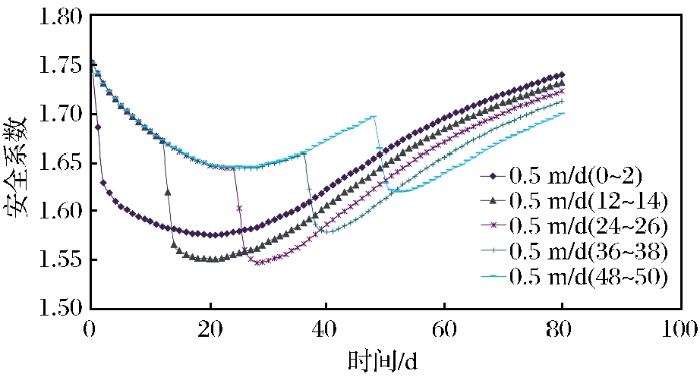
降雨发生在库水位骤降不同时刻稳定系数变化规律如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 稳定系数变化规律

Fig.8 Variation law of stability coefficient

平均型降雨发生在库水位骤降的不同时刻时，稳定系数总体上呈现先减小后增大的趋势，降雨时刻稳定系数突然下降，而当降雨发生在库水位骤降不同时刻时最小稳定系数并不相同。对于库水位骤降速率为0.5 m/d的情况下，当平均型降雨发生在库水位骤降第24~26 d时，最小稳定系数最小，为1.55，此时边坡处于最危险的状态。

4 结论

（1）库水位骤降情况下，孔压总体上随库水位下降呈现先减小后保持不变的趋势；随着边坡体内的监测点距库岸越远，孔压的变化幅度越小；边坡稳定系数总体上随时间呈现先减小后增大，之后再保持不变的规律，库水位下降速率越大，最小稳定系数越小且最小稳定系数出现的时间越早。

（2）不同静库水位耦合不同类型降雨情况下，孔压随时间呈现先增大后减小的规律；对于不同监测点来说，孔压达到最大的时刻略有差异；对于不同静库水位（155，165，175 m）来说，静库水位越高，整体孔压越大。

（3）库水位骤降情况下，边坡内部的孔压总体逐渐减小，但是在降雨过程中存在一个陡然上升的过程，孔压上升幅度大小排序为上部监测点≥中部监测点≥下部监测点；稳定系数总体上呈现先减小后增大的趋势，当平均型降雨发生在库水位骤降第24~26 d时，最小稳定系数最小，边坡处于最危险的状态。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘磊，殷坤龙，徐勇，等 .

考虑降雨及库水位变动的区域滑坡灾害稳定性评价研究

［J］. 岩石力学与工程学报， 2018 ， 37 （ 2 ）： 403 - 414 .